백준 1010번 (다리놓기) c++
문제

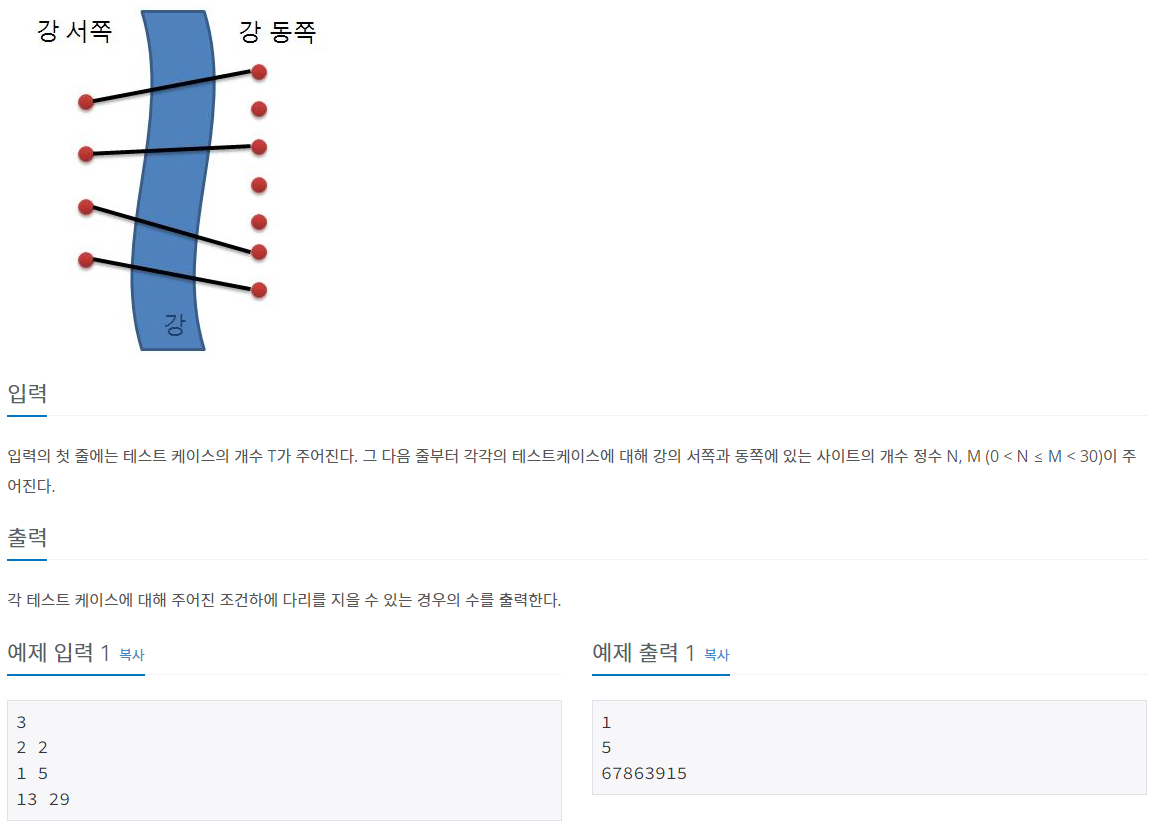
문제풀이
이 문제는 두가지 방식으로 풀 수 있다.
1. 조합
2. DP
1. 조합
nCr 서로 다른 n개 중 r개를 뽑는 경우의 수를 조합

예를 들어 A, B, C, D, E 5명의 후보가 존재할 경우, 2명의 대표를 뽑는 경우의 수는?
(A, B), (A, C), (A, D), (A, E)
(B, C), (B, D), (B, E)
(C, D), (C, E)
(D, E)

답은 10이 된다.
현재 문제에 적용을 시켜보면 n = C, r = N가 된다.
코드
#include <bits/stdc++.h>
using namespace std;
unsigned long long dp[101];
unsigned long long fact(int n){
if(dp[n]){
return dp[n];
}
else{
dp[n] = n * fact(n - 1);
return dp[n];
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
for(register int i = 0; i < T; i++){
int N, M;
cin >> N >> M;
dp[1] = 1;
if(N == M){
cout << "1\n";
continue;
}
cout << fact(M) << ' ' << fact(M-N) << ' ' << fact(N) << '\n';
unsigned long long result = fact(M) / (fact(M-N) * fact(N));
cout << result << '\n';
}
return 0;
}위와 같이 코드를 짜면 틀린다.
왜냐하면 fact(M-N) * fact(N) 을 계산할 수 없다. (정수 범위를 넘어간다.)
그래서 우리는 다른 방법으로 접근해야 한다.

nCr을 풀어 쓰면 위와 같은 식이 된다.
그래서 위 식과 같이 코딩을 하려면 반복문을 이용하여 구현할 수 있다.
코드
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
for(register int t = 0; t < T; t++){
int N, M;
cin >> N >> M;
int result = 1;
int temp = 1;
for(register int i = M; i > M - N; i--){
result *= i;
result /= temp++;
}
cout << result << '\n';
}
return 0;
}
2. DP
이 문제는 DP로도 풀 수가 있다.
파스칼의 삼각형의 형태와 같다.
예를 들어 N = 1, M = 1일 경우, 경우의 수는 1개이다.

N = 1, M = 2 일 경우, 경우의 수는 2개이다.

N = 2, M = 3 일 경우, 경우의 수는 3개이다.

N = 2, M = 3일 경우를 자세히 보자
이미 다리를 하나 놓은 경우, N = 1, M = 1 일 경우와 같다.
그리고 나머지 다리를 하나 더 놔야 하는데, 이 경우는 N = 1, M = 2의 경우와 같다.

그래서 N = 2, M = 3 인 경우는
(N = 1, M = 2 경우) + (N = 1, M = 1 경우) = (N = 2, M = 3 경우)
이렇게 볼 수 있다.
그리고 N = 2, M = 4 인 경우를 보자

원래라면
(N = 1, M = 3 경우) + (N = 1, M = 2 경우) + (N = 1, M = 1 경우) = (N = 2, M = 4 경우)
아래 식처럼 치환 할 수 있다.
(N = 1, M = 3 경우) + (N = 2, M = 3 경우) = (N = 2, M = 4 경우)
왜냐하면 이미 (N = 2, M = 3 경우)는 구하였기 때문이다.
그래서
DP[1][1] = 1 DP[1][2] = 2 DP[1][3] = 3 DP[1][4] = 4
DP[2][1] = 1 DP[2][2] = 1 DP[2][3] = 3 DP[2][4] = 6
DP 테이블을 이렇게 나타낼 수 있다.
DP 테이블을 이용하여
DP[i][j] = DP[i - 1][j - 1] + DP[i][j - 1] 이라는 식을 도출해낼 수 있다.
코드
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
int N, M;
int dp[31][31] = {0,};
for(register int t = 0; t < T; t++){
cin >> N >> M;
for(register int i = 1; i <= M; i++){
dp[1][i] = i;
}
for(register int i = 2; i <= N; i++){
for(register int j = 2; j <= M; j++){
dp[i][j] = dp[i-1][j-1] + dp[i][j-1];
}
}
cout << dp[N][M] << '\n';
}
return 0;
}